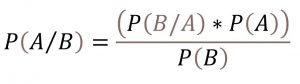The concept of the Dunning-Kruger effect is based on a 1999 paper by Cornell University psychologists David Dunning and Justin Kruger, which focused on logical reasoning, grammar, and social skills.

The Dunning-Kruger effect is a cognitive bias in which people with low ability at task or people with limited competence in a particular domain overestimate their ability, while people with high ability at task underestimate their ability.

The Dunning-Kruger effect is sometimes misinterpreted in popular culture as a generalization about the overconfidence of low-IQ individuals rather than the specific overconfidence of individuals who lack proficiency in a particular task.

Causes the Dunning-Kruger effect

Regarding the cause of the Dunning-Kruger effect, there are differing opinions.

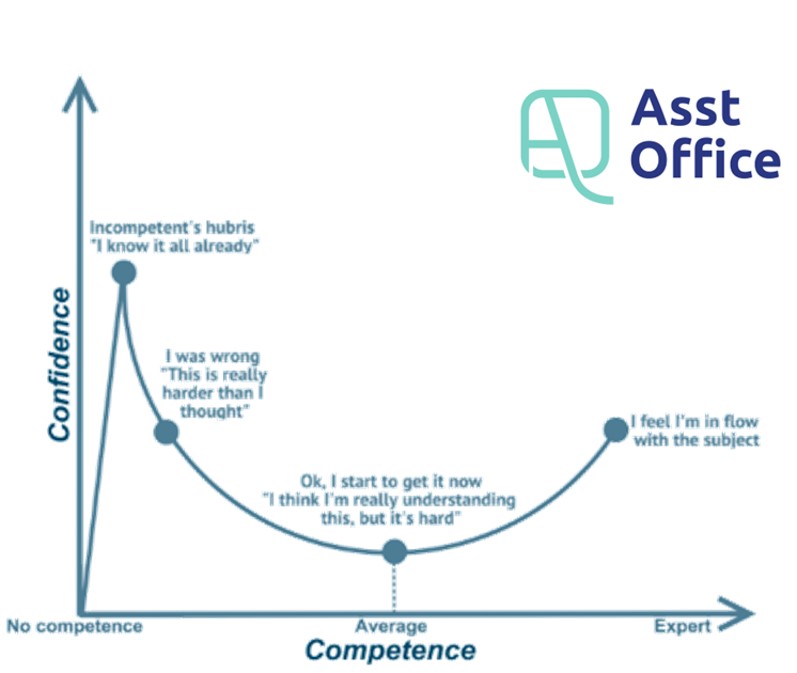
The researchers attributed the trend to a problem of metacognition—the awareness of your thought process.

“Those with limited knowledge in a domain suffer a dual burden: not only do they reach mistaken conclusions and make regrettable errors, but their incompetence robs them of the ability to realize it.”

In other words, poor performers misjudge their abilities because they fail to recognize the qualitative difference between their performances and the performances of others.

The actual results are explained by the statistical model as a statistical effect combined with the inclination to believe oneself to be better than average.

According to the rational model, inaccurate self-evaluation stems from excessively favorable past views about one’s abilities.

Another theory holds that because many low performers have very similar ability levels, self-assessment is more challenging and prone to errors for them.

Ignorance is sometimes bliss

Not every explanation of the Dunning-Kruger phenomenon emphasizes its negative aspects. Some also focus on its advantages, such as the fact that ignorance can occasionally be bliss. In this way, overconfidence may enable people to accomplish even seemingly impossible ambitions, while optimism can help them see the bright side of their circumstances. Preparatory planning and plan execution are two critical stages that have been proposed to be crucial for achieving a goal to separate the positive from the negative.

Dunning claims that excessive confidence can help during the execution stage by increasing motivation and energy. However, it can be harmful during the planning stage if the agent chooses to overlook poor odds, take unnecessary risks, or neglect to make backup plans.

 

 

In the financial industry, the Dunning-Kruger effect can arise when individuals who lack substantial knowledge and experience think they are very talented. Many risky actions, including aggressive trading, disregarding diversification, and underestimating potential losses, can result from overconfidence. Investors may find the illusion of knowledge to be a dangerous companion, especially in erratic markets where unanticipated events can quickly deplete wealth.

Source: Britannica, Psychology Today, The Decision Lab, AsstOffice

A mathematical method for calculating conditional probability that is based on a previous outcome that occurred in similar circumstances is known as Bayes’ Rule, after the British mathematician Thomas Bayes of the 18th century. The rule is also called Bayes’ Theorem or Bayes’ Law and is the foundation of the field of Bayesian statistics.

Understanding the Bayes’ Rule

Although the Bayes’ Rule is mostly used in the finance sector, where it can be used to rate the risk of lending money to potential borrowers, it is not limited only to this sector and is widespread. For instance, by taking into account the general accuracy of the test and the likelihood that a particular individual will have an illness, Bayes’ Rule can be used to assess the accuracy of medical test findings. To produce posterior probabilities, Bayes’ Rule depends on incorporating prior probability distributions. In Bayesian statistical inference, prior probability refers to the likelihood of an event transpiring before the collection of new data. Put another way, it stands for the most logical estimation of the likelihood of a specific result based on available information before the conduct of an experiment.

Thus, depending on new data that is or might be relevant to an event, Bayes’ Rule provides the likelihood of that event. The method can also be used to calculate the potential impact of hypothetical new information on the probability of an event occurring, assuming that the new information proves to be accurate.

The Formula

​Where:

P(A/B) is the probability of event A occurring, given that event B has occurred

P(B/A) is the probability of event B occurring, given that event A has occurred

P(A) is the probability of the event A

P(B) is the probability of the event B

In other words, Posterior equals (Likelihood)*(Prior) over (Marginal).

Example

Let us say P(Fire) means how often there is fire, and P(Smoke) means how often we see smoke. Then:

• P(Fire|Smoke) means how often there is fire when we can see smoke
• P(Smoke|Fire) means how often we can see smoke when there is fire

So the formula kind of tells us “forwards” P(Fire|Smoke) when we know “backwards” P(Smoke|Fire)

Source: Investopedia, Corporate Finance Institute, Stanford Encyclopedia of Philosophy, AsstOffice