A mathematical method for calculating conditional probability that is based on a previous outcome that occurred in similar circumstances is known as Bayes’ Rule, after the British mathematician Thomas Bayes of the 18th century. The rule is also called Bayes’ Theorem or Bayes’ Law and is the foundation of the field of Bayesian statistics.
Understanding the Bayes’ Rule
Although the Bayes’ Rule is mostly used in the finance sector, where it can be used to rate the risk of lending money to potential borrowers, it is not limited only to this sector and is widespread. For instance, by taking into account the general accuracy of the test and the likelihood that a particular individual will have an illness, Bayes’ Rule can be used to assess the accuracy of medical test findings. To produce posterior probabilities, Bayes’ Rule depends on incorporating prior probability distributions. In Bayesian statistical inference, prior probability refers to the likelihood of an event transpiring before the collection of new data. Put another way, it stands for the most logical estimation of the likelihood of a specific result based on available information before the conduct of an experiment.
Thus, depending on new data that is or might be relevant to an event, Bayes’ Rule provides the likelihood of that event. The method can also be used to calculate the potential impact of hypothetical new information on the probability of an event occurring, assuming that the new information proves to be accurate.
The Formula
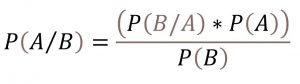
Where:
P(A/B) is the probability of event A occurring, given that event B has occurred
P(B/A) is the probability of event B occurring, given that event A has occurred
P(A) is the probability of the event A
P(B) is the probability of the event B
In other words, Posterior equals (Likelihood)*(Prior) over (Marginal).
Example
Let us say P(Fire) means how often there is fire, and P(Smoke) means how often we see smoke. Then:
- P(Fire|Smoke) means how often there is fire when we can see smoke
- P(Smoke|Fire) means how often we can see smoke when there is fire
So the formula kind of tells us “forwards” P(Fire|Smoke) when we know “backwards” P(Smoke|Fire)
Source: Investopedia, Corporate Finance Institute, Stanford Encyclopedia of Philosophy, AsstOffice


